Zijn Ratios wel Rationeel?

Deze vraag is heel terecht, want de meeste muziekliefhebbers verkeren niet in de gelukkige situatie dat ze de afmetingsverhoudingen of ratios van hun luisterruimte zelf konden kiezen op grond van akoestische en bouwkundige overwegingen.
Dat maakt de vraag legitiem: heeft het überhaupt zin om je met ratios bezig te houden in een thuissituatie?

Het antwoord is beslist "ja". Dat komt in de eerste plaats omdat het, ook bij reeds bestaande ruimtes, altijd zinvol is om te weten hoe goed of hoe slecht de bestaande verhoudingen precies zijn.
Ongunstige ratios kunnen een belangrijke en hardnekkige oorzaak zijn voor menig structureel probleem met de laagweergave in een muziekruimte. Zelfs met veel aandacht voor een goede luidsprekeropstelling kunnen dergelijke problemen nog manifest blijven! Je kunt in een gegeven situatie daarom maar beter weten waar de/een bron van laagproblemen precies ligt. Kennis over ratios van je ruimte is zodoende behulpzaam bij het stellen van de correcte diagnose omtrent weergaveproblemen.

In de tweede plaats is het zo dat een bestaande ruimte met ongunstige ratios soms relatief eenvoudig omgebouwd kan worden tot een ruimte met gunstige verhoudingen!
Dat zal al het geval kunnen zijn na het plaatsen van één extra muur! De fundamentele voorwaarde voor zo'n maatregel is natuurlijk wel dat een ruimte voldoende groot is om zo'n verkleining tot optimale verhoudingen toe te staan.

Ratios zijn dus bepaald niet vergezocht.
In elke bestaande situatie is het nuttig om te weten hoe zulke verhoudingen er precies bij liggen.
Succesvolle aanpak van alle vormen van akoestische problematiek vereist natuurlijk eerst kennis van de oorzaak. Zonder correcte diagnose kan er nooit een adequaat medicijn worden voorgeschreven...

De lengte, breedte en hoogte van een ruimte vormen samen de ratio.
Het zijn primaire parameters, bepalend voor het gegeven welke staande golven er op welke plek in de ruimte zullen optreden. Dit patroon van staande golven of ruimteresonanties is op zijn beurt één van de bepalende factoren voor de aanwezigheid van sterke pieken en/of dalen in de weergave van lage frequenties (alles onder 250 à 300HzHz is "laag" in de context van dit artikel).

Het patroon van ruimteresonanties kan in een gegeven ruimte door enkele eenvoudige berekeningen in kaart worden gebracht. Zo kan dus ook het patroon van een nog niet bestaande ruimte in kaart worden gebracht. Ook kan er zo op voorhand actief worden gezocht naar de meest optimale verhoudingen voor een toekomstige muziekruimte, binnen de grenzen die je als bouwer moet stellen.

Met behulp van een geschikte rekenmodule is het daarnaast eenvoudig, maar wel tijdrovend, om op voorhand een driedimensionale ruimte te definiëren die over een aanvaardbaar of zelfs optimaal patroon van staande golven beschikt.

Op de "downloadpagina" van deze site is onder punt-2 onder andere een rekenmodule te vinden waarmee ik altijd ratioberekeningen voor klanten uitvoerde. Met deze module zal ik ook de rekenvoorbeelden in dit artikel uitwerken. Bruikbare aanwijzingen voor het gebruik van de module worden zodoende met de tekst verweven. Voor het overige heeft het programma mogelijk een steile leercurve die eerst bedwongen moet worden om er soepel mee te kunnen werken. Dit artikel hoopt hieraan bij te kunnen dragen. Eenmaal bedwongen zal het mogelijk zijn om binnen elke footprint een ruimte met optimale verhoudingen te vinden.





Betere Ratios in een bestaande ruimte

Hierboven werd al opgemerkt dat zelfs een bestaande ruimte die niet over gunstige ratios beschikt daar in principe wel over kan gaan beschikken. De voorwaarde is natuurlijk wel dat de ruimte groot genoeg is om een zekere verkleining tot ideale ratios mogelijk te maken.

De foto rechts laat een voorbeeld zien waarin dit met groot succes kon worden uitgevoerd. Door de lengtemaat enigszins te verkorten ontstonden nieuwe, zeer gunstige afmetingsverhoudingen.

Het is soms mogelijk om, door het ietwat verkleinen van de lengte en/of de breedte, weliswaar op een iets kleinere ruimte uit te komen, maar dat is dan wel een ruimte die ineens over goede ratios kan beschikken.

Verkleinen betekent in de praktijk dan het plaatsen van een stenen binnenmuur, zodat de aanbeveling dat de grootte van de ruimte dit moet toestaan wel logisch is. Maar als die ruimte er is, kan verkleining tot optimale ratios veel opleveren.

Het verschil tussen goede en slechte ratios is soms maar een halve decimeter verschil in 2 van de 3 dimensies. In de foto rechts volstond het om uitsluitend de toch al overdreven lengtemaat met 73,5cm te reduceren. Het is daardoor niet absurd om te stellen dat optimale ratios best haalbaar kunnen zijn binnen een reeds bestaande ruimte.

Overigens dient hier vermeld te worden dat ratioberekeningen alleen met goed gevolg kunnen worden uitgewerkt voor een ruimte die beschikt over regelmatige (parallelle) afstanden.
Ratioberekeningen werken niet goed voor ruimtes die een onregelmatig gevormd grondoppervlak hebben, of die over anderszins verlopende lengte-, breedte- of hoogtematen beschikken.

Wat is een staande golf?

De animatie rechts laat zien hoe een staande golf ontstaat uit twee verschillende golven, die zich door de ruimte heen verplaatsen.
Als twee sinusvormige golven van gelijke frequentie (en dus gelijke golflengte) in tegengestelde richting reizen in hetzelfde medium, dan zal door hun superpositionering de netto beroering in het medium de som zijn van de twee golven.
Aan het fluctuerende punt kun je zien dat, indien beide golven 180° met elkaar uit fase zijn, zij elkaar uitdoven. En wanneer ze in fase zijn versterken ze elkaar.
Dat is het wezen / de essentie van een (problematische) staande golf.

Terwijl beide golven 'door elkaar heen reizen' in tegengestelde richtingen, fluctueert het netto resultaat tussen nul en een of andere maximale uitslag (amplitude).
Echter, dit patroon fluctueert of oscilleert slechts!
Het reist NIET van links naar rechts maar blijft op zijn plek STAAN.

Een klein eindje links ervan zie je een niet-fluctuerend punt.
Daar is geen probleem met een staande golf merkbaar!

Dergelijke plekken worden gedefinieerd door zowel de golflengte als de afmetingsverhoudingen
van het begrensde medium, in dit geval dus de wanden van een muziekruimte.


naar boven

de fysieke locaties van axiale staande golven in een ruimte
van 926 x 676 x 313 cm
de berekening is uitgevoerd met de module "roommodes.xls"

het midden van een ruimte is eigenlijk niet
de beste plaats om te gaan zitten luisteren

tegelijkertijd kiest men meestal terecht voor het handhaven van symmetrie,
door in het midden van de breedtemaat plaats te nemen
(bij opstelling in de lengterichting van de ruimte)












plaatsing van een nieuwe, gemetselde voorwand
reduceerde de lengtemaat met 73,5 cm,
maar gaf er een optimale ratio voor terug !

hoe een staande golf ontstaat en eruit ziet

Links: een ruimte met een goede ratio die zich leent voor verdere optimalisatie. Het basiskenmerk is een zo hoog mogelijke
"onderste probleemfrequentie". Die ligt hier op 56Hz.

Rechts: een ruimte met ongunstige (onbruikbare) ratios. Verdere optimalisatie zal zinloos zijn, om redenen die door verder lezen vanzelf duidelijk worden. Onderste probleemfrequentie: 31Hz

Hoe herken je optimale ratios?

Het allerbelangrijkste om steeds voor ogen te houden is dit:

In ruimtes met geweldige ratios zullen evenveel staande golven (resonantiemodi)
voorkomen als in ruimtes met gebrekkige ratios.

Goede ratios hangen dus niet af van de afwezigheid van resonantiemodi.
Afwezigheid van resonantiemodi kan simpelweg niet bestaan. Dit begrip is cruciaal.

Om de ratios van verschillende ruimtes onderling te kunnen vergelijken moeten ze zeker wel over een min of meer gelijke inhoud beschikken (binnen 5-10%). Het is niet zinvol om de ratios van een ruimte van 60 kuub te gaan vergelijken met die van een ruimte van 250 kuub.

De grotere ruimte zal door zijn grotere inhoud beduidend meer resonantiemodi bezitten dan de kleinere ruimte.
Daardoor zal de grote ruimte vanzelf veel hoger kunnen "scoren" volgens de beoordeling van de rekenmodule, maar een hogere score betekent hier alleen maar iets, wanneer ook de inhoudsmaten vergelijkbaar zijn!
Ondanks een lagere score kan de kleinere ruimte toch over veel betere verhoudingen beschikken...

Als de inhouden van ruimtes ongeveer gelijk zijn, dan zullen er zowel in goede als in slechte ruimtes ongeveer evenveel ruimteresonanties voorkomen.
Het aantal resonanties is daarom niet maatgevend voor de kwaliteit van de ratio.

Aan de hand van een voorbeeldruimte zal ik in dit artikel diverse berekeningen uitwerken.
Daardoor zullen de principes en criteria voor goede en slechte ratios vanzelf duidelijk worden.
De rekenmodule die hiervoor wordt gebruikt en die in de download is opgenomen heet "dimensional analysis_org.xls"

Overigens werd de voorbeeldruimte in kwestie ook daadwerkelijk gebouwd.
Het is uiteindelijk een compromisloze muziekruimte geworden.
Een uitgebreid fotoverslag van de bouw en afwerking is HIER te vinden.





Laagste Probleemfrequenties vergelijken

Bestudeer beide tabellen links nauwkeurig in relatie tot het onderstaande...

De ruimte die in de meest linkse tabel wordt getoond beschikt reeds over behoorlijk goede ratios, veelbelovend genoeg om wat verder mee door te rekenen.
De netto binnenmaten zijn 9,3 x 6,8 x 3,2 m, een volume van 196 kuub.

De ruimte in de rechtse tabel beschikt over zodanig ongunstige ratios, dat verdere doorrekenen niet zinvol is.
De netto binnenmaten zijn 11,3 x 5,7 x 3,2 m. Het volume is 206 kuub.
Deze inhoudsmaten liggen echter zo'n 5% van elkaar en maken het dus mogelijk om betrouwbare en directe vergelijkingen te maken tussen beide ruimtes.

De twee tabellen laten verder zien dat er onder 300Hz in totaal 479 samenvallende resonantiemodi (coincidences) optreden in de ruimte met de goede ratios, en 433 in de ruimte met de slechte ratios. Omdat deze laatste over meer inhoud beschikt zouden er ook meer resonantiemodi behoren te zijn, maar dat is niet het geval: dit is een eerste indicatie dat er van minder goede ratios sprake is.

Zoals gezegd worden gunstige of ongunstige ratios niet primair bepaald door het totaal aantal resonanties of staande golven in een ruimte.

De opsommingen bovenaan de twee tabellen tonen tevens aan dat er resp. 25 en 24 axiale modi zijn onder 300Hz, en dat in beide ruimtes 6 van die 25, resp. 24 modi een lagere frequentie dan 165Hz hebben.

Afgezien van het totale aantal modi zien we hier dus bijna gelijke cijfers in beide ruimtes. Toch beschikt er maar één over behoorlijk gunstige, en de andere over feitelijk onbruikbare verhoudingen.

Eén van de cruciale verschillen in kwaliteit wordt zichtbaar in de onderhelft van de twee tabellen.
In de goede ruimte ligt de laagste potentiële probleemfrequentie op 56Hz.
Probleemfrequenties zijn gemerkt met een X.
De minder goede ruimte, rechts, heeft op 30,5Hz zijn laagste potentiële probleemfrequentie!

Beide ruimtes krijgen, door hun lengte, vanzelf al een vrij lage potentiële onderste probleemfrequentie. Toch zal het verschil tussen 30,5Hz en 56Hz veelbetekend kunnen zijn, voor wat betreft het werk dat achteraf gedaan moet worden om potentiële problemen ermee op te lossen.
Er zijn veel diepere en meer volumineuze hulpmiddelen nodig om een probleem rond 30Hz te neutraliseren dan om datzelfde te doen voor een probleem rond 56Hz. Deze 56Hz is sowieso all een relatief hoge onderste probleemfrequentie in een grotere muziekruimte!

De laagste onderste probleemfrequentie is echter nog altijd niet de belangrijkste reden dat de linker ruimte over goede ratios beschikt en de rechter niet......

hierboven: gunstige ratios

• Resonantiemodi zijn regelmatig verdeeld.

• Onder t.b. 40Hz zijn ze geheel afwezig

• Boven t.b. 40Hz neemt het aantal modi gelijkmatig toe.

Het Grootste Gewicht

De factor waaraan het zwaarste gewicht wordt toegekend bij de beoordeling of een ratio akoestisch gunstig of ongunstig is betreft de verdeling van de staande golven over de lage frequentieband.

Deze "lage frequentieband" omvat de tertsbanden (1 tertsband = 1/3 oktaaf) onder 300Hz,
zoals deze op de verticale assen van de grafiek links zichtbaar zijn.

De ruimte uit de tabel linksboven is nu in de afbeelding links te zien en toont een goede verdeling van staande golven over het lagetonengebied. Dit kenmerkt zich op de volgende manier:

De tussenruimtes tussen de resonanties zijn gelijkmatig.
Dat betekent dat zich geen groepjes met staande golven vlakbij elkaar ophouden.
Evenmin zijn de modi zover van elkaar verwijderd dat er een tussenliggende tertsband helemaal vrij blijft van resonanties.
Dit kenmerk is niet links zichtbaar, maar wel in de tabel linksboven.

Per tertsband, met het stijgen van de frequentie, neemt het aantal resonanties snel toen.
Dat is zowel in goede als in slechte ruimtes het geval, en dat is ook de bedoeling.
Dit kenmerk is wel zichtbaar in de linkse tabel.

Het zou echter zeer ongunstig zijn, wanneer met het stijgen van de frequentie, dus met een volgende tertsband, het aantal staande golven zou afnemen!
Het aantal resonantiemodi moet in elke volgende tertsband ofwel toenemen, ofwel gelijkblijven.
Dat is in de tabel links het geval.

Een afname van modi tov een links naastliggende tertsband wordt een retromodus genoemd.
Een retromodus is een funest kenmerk, waardoor gebruik van die ratio niet wenselijk is.

In grafiek hier links zie je dus de ruimte met de gunstige ratios.
Het aantal resonanties blijft gelijk of neemt toe met het stijgen van de frequentie.

In deze ruimte is daarom geen retromodus aanwezig, waardoor het in elk geval lonend kan zijn om met de rekenmodule te bekijken of verdere optimalisatie mogelijk zal zijn.

hierboven: ongunstige ratios

• Resonantiemodi zijn onregelmatig verdeeld.

• Resonantiemodi blijven niet gelijk of lopen op, maar reduceren in aantal tussen sommige t.b. (retromodi).

• De fundamentele resonantie van de ruimte (f1) doet van zich spreken in t.b. < 20Hz.

• De toename van resonanties vlakt af tussen 63 en 80Hz.

De ruimte uit de tabel rechtsboven is nu in afbeelding links te zien en toont een slechte verdeling van staande golven over het lagetonengebied. Die slechte verdeling kenmerkt zich op de volgende manier:

Het eerste wat opvalt is dat het aantal resonantiemodi niet toeneemt bij elke tertsband.
Er is een reductie van het aantal resonanties te zien, ofwel een retromodus,
en wel tussen de tertsbanden 20 en 25Hz.
Een tweede retromodus is te zien tussen de tertsbanden 31,5 en 40Hz.

Daarnaast loopt, tussen de tertsbanden van 40 tot 63Hz, het aantal modi relatief snel op, zoals dat ook de bedoeling is, maar tussen de tertsbanden 63 en 80Hz vlakt die toename ineens bijna af, en dat is niet heel gunstig.

Dit is een schoolvoorbeeld van wat er met een slechte verdeling van staande golven wordt bedoeld.
Je kunt hierdoor in de eenmaal voltooide muziekruimte, tijdens het luisteren, problemen in de overdracht verwachten onder 20Hz, maar ook rond 30-35Hz en rondom 60Hz.

Al met al zijn dit teveel potentiële problemen waarmee je achteraf wellicht moet afrekenen.

Aangezien we ons hier nog altijd in het prille stadium van voorberekeningen bevinden, is het beter om een ruimte als deze te mijden, temeer omdat er altijd alternatieven zijn die (veel) betere resultaten beloven.





Wat zou je nu van dit alles merken?

In de praktijk zal het nu getoonde verschil tussen goede en slechte ratios zich altijd het duidelijkst manifesteren in de laagweergave. Maar dat is ook precies het deel van het frequentiespectrum dat we juist akoestisch willen optimaliseren door zo bezig te zijn met de keuze voor optimale verhoudingen.

De invloed van goede ratios komt eigenlijk alleen maar tot uiting in frequenties onder 300Hz.

De meest nare eigenschap van de retromodi in de ongunstige ruimte is, dat ze zich sterk onafhankelijk van de gekozen opstelling van luidsprekers en luisterplaats kunnen manifesteren.
Ondanks een geoptimaliseerde opstelling waar niets op aan te merken zal zijn, zal het meestal zo zijn dat er dankzij deze retromodi een sterke, onontkoombare signatuur wordt opgelegd aan de weergave van het laag. In dit geval zullen er rondom 20 en juist onder 35Hz zulke problemen zijn. Problemen rond een retromodus zullen altijd manifest zijn, wat je verder ook probeert. Als ze zo laag liggen als hier het geval is, krijg je gegarandeerd problemen met grotere luidsprekersystemen.
Jammer, maar gelukkig ook vermijdbaar, en dat is wel zo fijn als je een totaal nieuwe ruimte uit de grond gaat stampen.

Er zal altijd een gebrek aan laagdefinitie en strakheid kunnen samenhangen met muziekweergave in een ruimte met zulke ongunstige verhoudingen. Er is meer ongecontroleerde lagetonenenergie en een min of meer vermoeiende algehele basweergave merkbaar.

De ruimte die gunstige verhoudingen bezit zal zich daardoor neutraler gedragen in het laag, want bovenstaande nadelige eigenschappen zullen zich hier niet manifesteren. Er zijn immers geen retromodi die, dat wil ik nog eens benadrukken, boven alles vermeden moeten worden.
Eventuele probleemfrequenties die er wel zijn zullen hoger in de frequentieband liggen en milder van uitwerking zijn (axiaalmodi), waardoor ze gemakkelijker te temmen zijn dan echte lage probleemfrequenties en retromodi.

Maar let op: los van dit alles blijft het wel degelijk altijd mogelijk om een prachtige geluidsinstallatie zodanig slecht op te stellen in een ruimte met fraaie verhoudingen, dat ook hier het laag bijzonder belabberd kan klinken!
In aanleg en met de juiste kennis en aandacht is in zo'n ruimte echter veel gemakkelijker een goed en gedefinieerd laag neer te zetten.


naar boven

Boven: overzicht van de belangrijkste gegevens van de voorbeeldruimte met de gunstige ratios.

Merk op dat het enige verschil van betekenis met de andere ruimte hieronder het aantal "1/3 oktaaf retros" ofwel retromodi lijkt te zijn.
Ook is te zien dat deze iets kleinere ruimte toch over meer resonantiemodi beschikt, wat een voordeel is (verderop meer).
De ruimte krijgt een score van 219 punten.
Dat is in deze context het equivalent van een krappe voldoende, want scores tot 800 of 1000 zouden haalbaar kunnen zijn bij deze inhouden.



Onder: een overzicht van de belangrijkste gegevens van de voorbeeldruimte met de ongunstige ratios.

Merk op dat het enige verschil van betekenis met de ruimte hierboven het aantal "retros" is.
Het rapportcijfer is hier een negatief getal, nl. -542.
En dat is wel het equivalent van een hele dikke onvoldoende.

Meer over vergelijken
met de Rekenmodule

De tot nu toe besproken en getoonde gegevens en conclusies kunnen worden verkregen met de rekenmodule "dimensional analysis_org.xls". De getoonde tabellen zijn screenshots uit die module.

Eén bruikbare kernfunctie van de module is zodoende het analyseren en beoordelen van één ratio tegelijkertijd.

Een tweede, minstens zo zinvolle kernfunctie, is het zoeken van gunstige ratios binnen tevoren gespecificeerde onder- en bovengrenzen.

Het resultaat van die kernfunctie is een tabel zoals hier links is te zien is -- de "dimensional suitability comparison". Deze tabel heeft overigens niets van doen met de voorbeeldruimte die we bespreken!

De tabel toont een reeks ratios (scenarios) met hun belangrijkste eigenschappen.
In de reeks wordt elk scenario voorzien van een puntenscore ter waardering.

Eerder werd al opgemerkt dat interpretatie en vergelijking van scores en analyses van gevonden ratios alleen mogelijk is, als de te vergelijken ruimtes over inhouden beschikken die ten hoogste 10% van elkaar verschillen.

In de praktijk van het zoeken en vinden van een optimale ratio voor je muziekruimte zul je kunnen uitgaan van maximale en minimale maatvoeringen voor lengte, breedte en hoogte. Je hebt tevoren een bepaalde maximale en minimale footprint voor je ruimte in gedachten, alsmede een bepaalde minimale en maximale hoogte die de ruimte mag krijgen, dit alles ivm je budget en de bouwnormen ter plaatse.
Het zou tamelijk ondoenlijk zijn om binnen zulke grensgebieden alle ratios één voor één te gaan zoeken en doorrekenen. De rekenmodule kan dit veel beter voor je doen, maar dan zul je 'm dus moeten "voeden" met minimale en maximale grenswaarden voor de toekomstige ruimte.

De locatie waarvoor nevenstaande berekening gemaakt werd is vrij extreem: je ziet dat de hoogtemaat tussen 500 en 526cm mag liggen. Ook zie je dat lengte en breedte aan grenzen gebonden zijn die duiden op een tamelijk vierkante footprint: het betreft hier een zeer fors thuistheater.
De rekenmodule zal trachten om, binnen de opgegeven grenzen, optimale verhoudingen te zoeken.
Dat is hier beslist gelukt...

• Merk allereerst op dat geen van de opgegeven onder- en bovengrenzen absurd of onrealistische ver uiteen liggen. De rekenmodule kan zoiets overigens ook niet aan, en zal 'weigeren' te rekenen indien je het rekenvermogen overstijgt.
  
  
• Berekeningen met zulke realistische en niet al te ver uiteenliggende boven- en ondergrenzen zullen scores opleveren die je goed met elkaar kunt vergelijken, aangezien de inhoudsmaten tamelijk gelijkwaardig zullen zijn. Denk eraan dat ze maximaal binnen 10% van elkaar moeten liggen.
  
  
• Het is niet verplicht om de drie grensgebieden L-B-H allemaal variabel te maken. Je mag ook best rekenen met een gefixeerde hoogte en alleen lengte en breedte laten variëren. Alle combi's zijn mogelijk.
  
  
• Tabellen met berekeningen binnen grensgebieden laten een opeenvolging zien van steeds beter wordende ratios (scenarios) - de beste staat altijd bovenaan en het scenario "preferred" is vetgedrukt.
  Overigens is dit een van de beste ratios die ik ooit kon vinden, met slechts één axiaalmodus (tevens dus de 'laagste' probleemfrequentie) op exact 100Hz...
  
  
• Je ziet in de tabel dat het aantal samenvallende axiaalmodi geleidelijk aan toeneemt. Pas bij 3 of meer gaat dat werkelijk ten koste van de gunstige score. Je ziet ook dat de verschijning van één enkele retromodus ineens veel punten kost in de beoordeling.
  
  
• Om te weten waar de laagste probleemfrequentie precies ligt zul je de individuele ratio moeten doorberekenen, zoals we nu hier links gaan doen met onze voorbeeldruimte.
  
  

Terug naar de voorbeeldruimtes

De twee tabellen links geven een "numerieke samenvatting" van het patroon van resonantiemodie in de berekende ruimtes. Ondanks de eenvoud kunnen er doorslaggevende conclusies worden getrokken op basis van deze analyse, zeker nu we weten waar we op moeten letten.

Axiaal samenvallende modi onder 165Hz en met name retromodi tellen altijd het zwaarst door in de score!
Boven 165Hz neemt het aantal modi zo snel toe, dat van een ongunstige verdeling of tussenruimte steeds minder sprake kan zijn. Daaronder is dat duidelijk wel het geval, vanwege hun geringe numerieke aantal.
Het aantal in de tabel genoemde modi (Axial) verwijst naar de samenvallende axiaalmodi onder 165Hz!
Eén ding is altijd zeker: hoe minder axiaalmodi onder 165Hz er zijn hoe beter, en ook: hoe hoger hun frequentie is, hoe beter dat zal uitpakken!

Tevens geldt in deze tabellen: hoe hoger het totaal aantal modi (Total Modes) uitvalt, hoe beter.
Dit kan tegenstrijdig lijken, maar is niettemin waar...
Het totale aantal modi is voor het grootste deel een direct gevolg van de inhoud: hoe groter de ruimte, hoe hoger het totale aantal modi zal zijn. We weten inmiddels dat meer modi automatisch gunstiger is: meer modi geven navenant veel meer kans op een fraaie en evenredige verdeling over de tertsbanden dan een handjevol modi dat kan bieden.

Nog een gegeven uit de tabellen: hoe lager tegelijkertijd ook het totaal aantal samenvallende modi (Coincident Modes) uitvalt, hoe beter dat zal zijn.
Hieruit volgt dus dat niet zozeer het totale aantal resonantiemodi erg doorslaggevend is, maar wel het totale aantal samenvallende modi.

Een samenvallende modus is altijd een staande golf, samengesteld uit twee resonantiemodi van nagenoeg gelijke frequentie (binnen 5% van elkaar). Deze kunnen optreden als resonanties die gelijktijdig door bijvoorbeeld de lengte en de breedte of de breedte en de hoogte worden aangesproken.
De enkelvoudige modi worden door één afmeting tegelijk aangesproken, en zij zijn in principe onschadelijk, op voorwaarde dat ze regelmatig kunnen worden verdeeld over de frequentieband onder 300Hz.

In het ergste geval kunnen er in een ruimte nagenoeg identieke samenvallende modi voorkomen, die zowel door lengte, breedte als hoogte tegelijk worden opgewekt.
Samenvallende modi worden aangesproken als lengte, breedte en hoogte in een bepaalde verhouding tot elkaar staan, bijv. wanneer de lengte (ongeveer) tweemaal zo groot is als de breedte, of als de hoogte een kwart is van de lengte of daaromtrent.

Over de zogenaamde "gouden ratio"

Akoestiek heeft in de volksmond altijd een zeker mythisch karakter gehad. Zelfs in deze tijd van vrijelijk beschikbare informatie blijven er niettemin twee mythes hardnekkig verankerd liggen in die volksmond, om steeds weer op te duiken. De eerste is de mythe van de eierdozen, waarmee men alle akoestische problemen zou kunnen oplossen. De tweede mythe is die van een "gouden ratio", als zou dit de enige juiste weg zijn naar goede afmetingsverhoudingen.

De eierdozenmythe is intussen wel grotendeels ingehaald door de praktijk. De meeste liefhebbers zijn op de hoogte van het bestaan van een variëteit aan specialistische akoestische hulpmiddelen voor het oplossen van uitdagingen rondom nagalm en reflecties.
De mythe van de gouden ratio heeft zijn aureool nog altijd kunnen behouden, maar mag in de context van dit artikel zijn voetstuk vallen...

De zogenoemde "gouden ratio" is:

1 : 1,9 : 1,4

Dat dit in relatie tot een bepaalde inhoudsmaat een goede ratio kan zijn is zeker waar. Vaak wordt echter gemeend dat deze verhouding ook de enig bestaanbare ideale zou zijn, van toepassing op alle willekeurige muziekruimtes.

Dat is gelukkig hele grote onzin...!

De verhouding 1 : 1,9 : 1,4 werd lang geleden door ene M.M. Louden gevonden in relatie tot een geslaagde openbare concertruimte. Deze ruimte was, onder andere maar niet uitsluitend door deze afmetingsverhoudingen, zozeer geslaagd, dat deze verhouding sindsdien als de gouden ratio bekend is gebleven, zowel bij akoestici en architecten als bij leken.

Gelukkig voor ons, liefhebbers thuis, zijn er nog heel wat meer heel goede optimale verhoudingen in deze wereld voorhanden. Dat is maar goed ook, want als je de gouden ratio gaat toepassen op ruimtes met een relatief kleine inhoud (<120 kuub), zoals die thuis worden aangetroffen, dan levert dit zeker niet altijd optimale verhoudingen op. Er kunnen hoogstens uitgangspunten ontstaan voor een verdere verfijning van de zoektocht.
De belangrijkste reden dat er gelukkig ook andere goede verhoudingen bestaan is gelegen in het (on)praktische nut van de gouden ratio: die is namelijk helemaal niet zo bruikbaar in thuissituaties.
Let maar eens op...

In de tabel rechts zie je "de twintig ideale ratios voor luisterruimtes en luidsprekerbehuizingen". Deze verhoudingen werden gedefinieerd door de heren Louden en Seppmeyer. Bovenaan het rijtje staat de beruchte gouden verhouding; de 19 andere daaronder zijn eveneens prima verhoudingen.

De factor "1" zul je zelf moeten definiëren in de berekeningen, zoals hier rechts is gedaan. Meestal ga je voor de factor-1 uit van de hoogtemaat, aangezien de andere twee verhoudingen van lengte en breedte groter zullen worden.

Hier rechts is factor-1 gelijkgesteld aan een hoogte van 313 cm.

De ideale ruimte volgens de gouden ratio zou bij een hoogte van 313cm dus een lengte van 595cm en een breedte van 438cm krijgen, wat een inhoud van 81,6 kuub oplevert. Voor thuisbegrippen zijn dat inderdaad realistische lengte- en breedtematen, maar de hoogtemaat is niet zo realistisch! Immers, waar vindt je tegenwoordig nog ruimtes die hoger zijn dan 3 meter?

En wat als we, zoals in het geval van onze voorbeeldruimte in dit artikel, eigenlijk op zoek zijn naar een ruimte met een grotere lengte en breedte? We zouden, om de gouden ratio te kunnen hanteren, de hoogte nog veel verder moeten vergroten en dat zal bouwtechnisch niet vanzelfsprekend zijn om allerlei redenen.
De "voorgebakken ratios" zijn heel vaak ronduit ontpraktisch voor thuis. Ze werden immers overgenomen uit de professionele wereld, die met heel wat grotere volumes rekent, en waarbij niet de normale gemeentelijke bouwverordeningen van toepassing zijn zoals bij jou, de gewone burger.

Onder de eerste gouden ratio rechts staan nog 19 andere gunstige verhoudingen. Ze kunnen allemaal dienen als uitgangspunt voor verdere analyse met de rekenmodule, want -- en dat is vooral ook de crux -- ze zijn niet per definitie goed bij alle inhoudsmaten!

De gekozen factor-1 van 313cm is dus niet direct een kamerhoogte die je zomaar thuis gaat aantreffen!
Moderne kamerhoogtes zullen ergens tussen 240 en 270cm liggen; kelderruimtes kunnen soms nog wel lager zijn! Door factor-1 (hoogtemaat) te reduceren, zullen ook de lengte en breedte navenant kleiner gaan worden. Het resultaat daarvan zie je in de volgende tabel, hier rechtsonder.

Wanneer de doorgaans onrealistische hoogte van 313 cm nu door een meer gangbare hoogte van 245 cm wordt vervangen, ontstaat een serie van 20 verhoudingen die, zelfs voor thuissituaties, een te kleine ruimte opleveren. Dat zijn meestal niet de serieuze muziekruimtes die je dedicated laat bouwen, tenzij je alleen zoiets als een slaapkamer over hebt voor de audio.

In de tabel rechts is de factor-1 nu gelijkgesteld aan hoogte = 245 cm.

Dankzij een meer gangbare plafondhoogte varieert de inhoud van ruimtes met deze voorgebakken ratios tussen 22 en 56 kuub. De gevierde "gouden ratio" heeft een inhoud van nog slechts 39 kuub en dat is niet bepaald veel...

Als er dus uitsluitend deze 20 ruimtelijke verhoudingen zouden bestaan, aangevoerd door de gouden ratio van 1 : 1,9 : 1,4 dan zou het tamelijk onmogelijk zijn om in thuissituaties een voldoende grote muziekruimte te bouwen met goede verhoudingen.

De moraal van dit verhaal is simpel: optimale ratios bestaan gelukkig ook helemaal los van nevenstaande 20 voorgebakken verhoudingen van Louden en Seppmeyer.

De Universiteit van Salford heeft in de jaren '80 baanbrekend onderzoek verricht op het gebied van afmetingsverhoudingen. Los van alle technische details is men daar ondubbelzinnig tot de conclusie gekomen dat er ontelbare goede ratios bestaan, maar dat zij even sterk gekoppeld zijn aan de resulterende inhoud als aan de op zichzelf staande drie dimensies lengte, breedte en hoogte.

Anders gezegd: bepaalde afmetingsverhoudingen zullen uitsluitend optimaal kunnen zijn binnen bepaalde inhoudsgrenzen. Daarbuiten kan diezelfde verhoudingen ook heel goed minder optimaal zijn, of gewoon hartstikke ongunstig! Het doorrekenen van een individuele verhoudingen met de rekenmodule laat dan onmiddellijk zien hoe het erbij staat met die ratio bij die inhoud.


naar boven

Ratios met Inhoud !

Het onderzoek van de Salford Universiteit bracht in de jaren '80 van de vorige eeuw radicaal nieuwe inzichten en conclusies voort op het gebied van ruimtelijke afmetingsverhoudingen.
De belangrijkste conclusies zijn hieronder samengevat:

• Het volume (de inhoud) van een ruimte is bepalend voor de toepasbaarheid van een bepaalde afmetingsverhouding.
  Ofwel: een verhouding die uitstekend toepasbaar is op ruimtes die beschikken over volumes tussen 50 en 70 kuub, kan minder geschikt of ongeschikt blijken voor ruimtes die over het dubbele of het drievoudige volume beschikken. Grotere muziekruimtes thuis beschikken over volumes van 125 kuub of meer.
  
  
• De in hun context geformuleerde afmetingsverhoudingen van Louden en Seppmeyer (de voorgebakken ratios van hierboven) zijn weliswaar goed te noemen, maar leggen vaak praktische beperkingen op aan de inhoud van de resulterende ruimte. Die inhoud is niet groot genoeg voor veel thuissituaties, tenzij de hoogte van zo'n ruimte een voor thuisbegrippen onrealistische waarde kan krijgen.
  Dit werd geïllustreerd met de voorbeelden hierboven, waarbij het moeilijk blijkt om de realistische kamerhoogte van een gemiddelde thuissituatie te koppelen aan realistische lengte- en breedtematen.
  
  

Eén van de fraaiste afmetingsverhoudingen die ik zelf ooit kon vinden in de zoektocht naar ideale maten voor een grote thuisbioscoop, steekt feitelijk de draak met de welbekende instructie dat een vierkant of bijna vierkant vloeroppervlak zou moeten worden vermeden. Zoals je waarschijnlijk al weet heeft een thuisbioscoop op grond van zijn gebruiksdoel meer baat bij een naar vierkant neigend vloeroppervlak voor optimale rondom-opstelling van de meerkanaals geluidsbronnen, terwijl een stereo (tweekanaals) muziekruimte meer baat heeft bij een rechthoekige grondvorm.

Hoe dan ook, de gevonden bioscoop in kwestie kreeg
de geweldig gunstige afmetingsverhoudingen van 800 x 738 cm,
gekoppeld aan een hoogte van 2,80 cm.

Als je deze afmetingen in de rekenmodule invoert (let op dat je dat in meters doet en niet in feet !), kom je erachter dat er in deze ruimte geen enkele axiale resonantiemodus onder 187Hz voorkomt. Vanzelfsprekend is er ook geen retromodus aanwezig, en evenmin zijn er andere dan axiale modi onder 165Hz, veroorzaakt door samenvallende resonanties.
Kortom: een zeldzame topratio met NUL potentiële probleemfrequenties, waar je nooit aan zou denken als je je had vastgepind op voorgebakken ratios en starre voorschriften.

De tabel rechts is een rekenvoorbeeld waarin de onderzoeksresultaten van Salford zijn meegenomen.

De uitkomsten kunnen gehanteerd worden als uitgangspunten voor ruimtes met inhouden van om en nabij 70 kuub (+/- 10%).
Voor ruimtes met meer of minder inhoud gelden in principe andere verhoudingen.
Voor ruimtes met beduidend grotere volumes (> 150 kuub) is dat eveneens zo.

In de tabel rechts is factor-1 wederom 245 cm kamerhoogte.

Nu blijkt dat er met een realistische hoogtemaat gelukkig ook muziekruimtes met een grotere footprint (= L x B) kunnen worden gevonden.

Maar voor alle duidelijkheid: in deze tabel zijn de volumes 11 t/m 18 bruikbaar als uitgangspunt, vanwege hun inhoud van 70 kuub.

De overige volumes kunnen eventueel ook uitstekend zijn, maar hun inhoud is meer dan 10% groter of kleiner dan 70 kuub, waardoor de kans op succes wat kleiner is, aldus Salford University.

Aangezien je sowieso altijd individuele ratios zult gaan narekenen, zal het geen enkel probleem zijn om dat te doen met een voor jou aantrekkelijke verhouding uit nevenstaande tabel, ook al is de gevonden inhoud niet overeenkomstig het uitgangspunt van 70 kuub...

Nu even alles samenvatten...

Elke goede ratio zal altijd moeten worden gekenmerkt door onderstaande eigenschappen tegelijkertijd:

• De laagste probleemfrequentie (samenvallende axiaalmodus of 'coincident axial mode' in de rekenvoorbeelden) zal vrij hoog liggen. Hoe hoger deze ligt, hoe gemakkelijker eventuele problemen ermee achteraf te neutraliseren zullen zijn.
  Streef bij het zoeken naar goede verhoudingen naar laagste probleemfrequenties die in elk geval boven 60Hz liggen. De praktijk wijst uit dat 100Hz of zelfs nog hoger ook prima haalbaar kan zijn. Vaak zul je lang moeten doorzoeken met de module, maar als ze er zijn zal de module ze ook kunnen vinden!
  
  
• Het totale aantal samenvallende axiale modi onder 165Hz zal gering zijn. Het liefst is hun aantal nul, maar een maximum van 3 van deze axiaalmodi zal niet tot grote problemen hoeven te leiden, mits hun frequentie hoog genoeg ligt (zoals het eerste kenmerk voorschrijft).
  
  
• Retromodi moeten (bijna) altijd worden vermeden. Hierover is feitelijk geen twijfel mogelijk.
  Er is één uitzondering, en dat is wanneer de retromodus in kwestie zodanig laag ligt, dat je luidsprekersysteem die lage frequentie nooit zal kunnen aanspreken. Een retromodus op 19Hz zal waarschijnlijk niet tot problemen leiden bij luidsprekers die over een -3dB-punt van 45Hz beschikken...
  In alle andere gevallen zal een uitstekende ratio met één retromodus je in een later stadium moeilijk of onmogelijk te elimineren narigheden opleveren. Liefst vermijden dus!

Als de laagste probleemresonantie, na verdere optimalisatie met de rekenmodule, voldoende hoog kan worden gelegd dankzij een goede combinatie van lengte, breedte en hoogte, zal strak ook de noodzaak om diep afgestemde basstraps en andere afgestemde absorbers in te zetten voor het elimineren van probleemfrequenties verdwijnen.
Een lagere probleemfrequentie vereist voor compensatie per definitie een diepere basstrap dan een hogere frequentie. We hebben het dan toch wel over decimeters toegenomen diepte, en niet zomaar over wat centimeters......

Overigens zal in een ruimte met goede verhoudingen niet de noodzaak verdwijnen om een goed en algemeen bass-management toe te passen! Wat dus wel verdwijnt is de noodzaak om, daarnaast, allerlei extra en zware maatregelen te nemen om probleemfrequenties op te lossen.

Samenvallende axiale modi geven de ruimte een sonische signatuur mee in het gebied van de lage tonen. Het is in sommige gevallen niet mogelijk om daar helemaal vanaf te komen, maar het is, door goed rekenen, wel goed mogelijk om van meet af aan te werken in een ruimte die geen sterke signatuur gaat opleggen door ongunstig gekozen ratios.

De samenvatting van het hele verhaal, zoals het tot nu toe is verteld,
wordt uitstekend inzichtelijk gemaakt in de twee afbeeldingen rechts.
Bestudeer ze goed...

naar boven

Zelf gaan bouwen?

Alvorens we verder gaan stoeien met de rekenmodule, om daardoor de gevonden, veelbelovende ratio van de voorbeeldruimte verder te vervolmaken, is het zinvol dat je eerst eens ruimte geeft aan het denkbeeld van een aannemer, die straks een ruimte komt neerzetten volgens jouw specificaties.

De vraag die je jezelf stelt is deze:

Welke praktische implicaties kom ik tegen, als ik de keuze maak
om zelf een ruimte met optimale ratios te laten bouwen?

Je wilt boven alles dat je aannemer jouw niet-alledaagse wensen omtrent de afmetingen en het belang daarvan heel serieus neemt -- even serieus als jij dit alles zelf zult nemen!

Dit onderdeel in het hele proces kun je maar één keer uitvoeren; dan maar beter goed...

Die aannemer zal zijn werk zodanig serieus moeten nemen, dat hij binnen nauwe toleranties kan en wil werken, om te voldoen aan jouw eisen aangaande lengte, breedte en hoogte van de ruwbouw.

De praktische implicaties en cruciale wetenswaardigheden worden in de kolom rechts in detail uitgewerkt.

Je moet er zelf in elk geval alles aan willen doen om de vooraf doorgerekende optimale verhoudingen daadwerkelijk in fysieke vorm over te brengen op het het bouwproject, anders krijgt al die moeite en de extra financiële investering maar heel weinig meerwaarde.

Het berekenen van fraaie afmetingsverhoudingen is één ding;
het implementeren ervan is iets anders.

Met name een goed overzicht en organisatietalent zijn nodig...

Ruwbouw in de praktijk...

De gekozen ratio waarmee je uiteindelijk je muziekruimte wilt uitrusten is een delicate verhouding. Een volledig geoptimaliseerde verhouding laat in de praktijk van het bouwen hoogstens een zeer minieme afwijking toe.
Dit moet nog wel nader genuanceerd worden...

Hoewel we spreken over een "ruwbouw" is ruw bouwen niet toegestaan...
Onnauwkeurig werken tijdens het realiseren van de ruwbouw is niet zo vergezocht als het lijkt. Bij onnauwkeurig werken kunnen er zomaar afwijkingen van + of - 1 cm in lengte- breedte- of hoogtemaat sluipen. Bij de hoogtemaat onstaan zulke afwijkingen gemakkelijk als de vloer niet volkomen vlak zal worden gelegd...

Een maximum van 1 centimeter afwijking in één dimensie
is meestal nog net geen probleem.

MAAR... als er, behalve een afwijking van die ene centimeter voor bijvoorbeeld de lengtemaat, ook nog een ogenschijnlijk kleine afwijking van opnieuw één centimeter in de breedte en mogelijk ook een van 2 cm bij de hoogte zou optreden, dan kan die combinatie van drie afwijkingen er helaas toe leiden dat de verhouding niet meer volkomen optimaal uitvalt.
Er ontstaat dan een (hopelijk milde) probleemfrequentie die eigenlijk niet is voorzien en ook eigenlijk niet nodig zou zijn.

Met andere woorden:
Een centimeter afwijking in één dimensie (L, B of H) is niet meteen het ergste wat je kan overkomen, maar als er in twee of alle drie de dimensies "kleine" afwijkingen optreden door onnauwkeurigheid tijdens het bouwen, zal de berekende ratio teveel gaan afwijken van het berekende doel.

Zoals gezegd is zulks vooral het geval met een maximaal geoptimaliseerde ratio, waarin NUL problemen met axiaalmodi optreden. Zo'n ratio is een delicate verhouding, omdat de probleemfrequenties zogezegd ook maar net buiten de deur kunnen worden gehouden.
De ratio zal er niet meteen bar slecht van worden, maar zal zeker minder goed worden dan werd verwacht!

Dit alles betekent in de praktijk gewoon, dat er tijdens de bouw geen afwijkingen in de opgegeven maatvoeringen zijn toegestaan!

Mijn 13 jaren van betrokkenheid bij en ervaring met dit soort bouwprojecten toonde gelukkig aan dat het, in ieder geval voor serieuze aannemers, goed mogelijk is om binnen bouwtoleranties van ten hoogste 3 mm te blijven.
Je zult de aannemer wel op voorhand al heel sterk moeten overtuigen van de noodzaak tot dit soort nauwkeurigheid, en ook proberen te 'zien' of dit echt bij hem binnenkomt en serieus genomen wordt! Alleen beleefd "ja meneer" horen zeggen is geen garantie voor succes.

Fouten en gevolgen van onnauwkeurigheid kunnen niet meer ongedaan worden gemaakt...
Kies bij twijfel over competenties gewoon maar voor een andere aannemer!






Bruto en Netto binnenmaten

Wanneer er een optimale ratio is gekozen die bouwtechnisch met voldoende maatnauwkeurigheid kan worden gerealiseerd, zul je van meet af aan onderscheid moeten maken tussen bruto en de netto binnenmaten.

Bruto binnenmaten...
... verwijzen naar de inwendige maatvoeringen van de ruwbouw zelf.


Netto binnenmaten...
... verwijzen naar de inwendige maatvoeringen van de voltooide binnenruimte,
dus compleet met de beoogde bouwtechnische en akoestische eindafwerking.

Een geoptimaliseerde ratio definieert de NETTO binnenmaten van een voltooide muziekruimte,
maar niet (persé) de bruto binnenmaten van de ruwbouw zelf!

Dit heeft als consequentie dat de bruto binnenmaten van je ruwbouw groot genoeg moeten zijn om,
pas na implementatie van de eindafwerking, de beoogde optimale verhoudingen op te leveren.






Bruto / Netto -- een voorbeeld met de hoogtemaat

De optimale hoogtemaat -- we gaan uit van 320 cm -- moet in de netto binnenruimte ontstaan, nadat het plafond van een eindafwerkingslaag is voorzien, en nadat de vloer op de definitieve woonhoogte werd gebracht.
Dat betekent dat de gezamenlijke dikte van bijvoorbeeld een natuurstenen of houten vloer, alsmede die van de stuclaag of andere eindafwerking van het plafond van de bruto binnenhoogte van de ruwbouw afgetrokken moeten worden.

Omdat de optimale binnenhoogte uiteindelijk 320 cm moet zijn, en er een natuurstenen vloer van 4cm dikte, alsmede een stuclaag van 1,5cm tegen het plafond zal worden aangebracht in de bruto binnenruimte, dient die bruto binnenhoogte ook minstens 6cm hoger te worden gebouwd dan de berekende ratio zelf voorschrijft.

Bij het uitvoeren van de juiste kamerhoogte hoeven in principe nooit afwijkingen te ontstaan. Door de vloer van de bruto ruwbouw professioneel te laten storten, kan deze volkomen vlak komen te liggen, waardoor elke hoogte door de juiste storthoeveelheid kan worden gerealiseerd. Ook het plafond zelf kan, dankzij moderne techniek, volkomen vlak komen te liggen.
Dit stadium komt tot uiting in de foto links.

Uiteraard zijn bovenstaande opmerkingen ook van toepassing op alle eindafwerkingen die de lengte en de breedte van de netto ruwbouw betreffen.
Alleen massieve eindafwerkingen zullen de bruto afmetingen verkleinen.
De overblijvende maten zullen na eindafwerking moeten corresponderen met de optimale ratio.






Bruto / Netto -- maar niet alles telt mee!!!

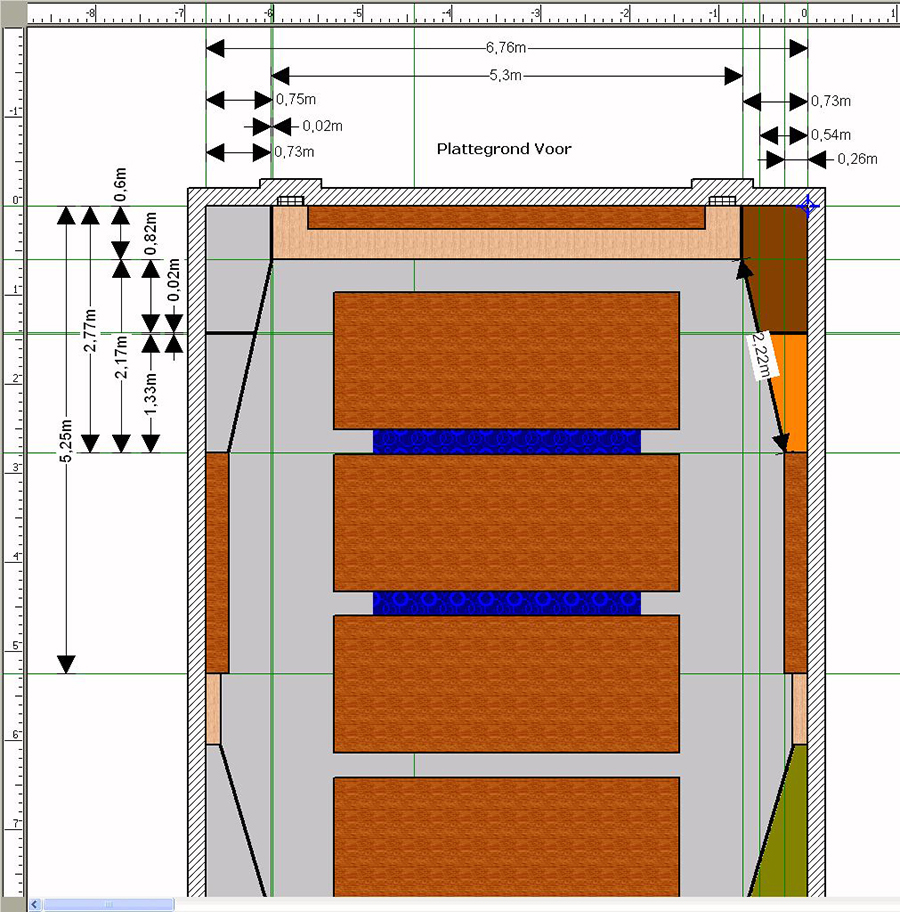
Om de navolgende opmerkingen goed te interpreteren kun je het beste de "plattegrond-voor" (van de voorbeeldruimte) in ogenschouw nemen.
Die kun je in de linkse kolom hieronder vinden.

In een volledig voltooide muziekruimte worden regelmatig akoestische eindafwerkingen voor plafonds en wanden toegepast die niet zozeer een massieve constructie bezitten, zoals de stenen wanden en de betonnen vloer en het plafond, maar die "zacht" zijn en behoren tot de zgn. buigslappe constructies.

Een verlaagd opgehangen akoestisch systeemplafond behoort bijvoorbeeld tot deze categorie van buigslappe constructies, evenals vrij in de ruimte opgehangen stoffen afscheidingen.

Buigslappe voorzetwanden met daarachter holle ruimtes, zoals je die in de plattegrond links kunt zien, horen ook tot de akoestische eindafwerking van een muziekruimte. Via de eerder genoemde fotoreportage van deze compromisloze muziekruimte zie je dat in de eindafwerking dergelijke staande voorzetwanden en basstraps zijn toegepast.

Dergelijke constructies zullen NIET de netto binnenmaten
van de ruwbouw, en dus ook niet die van de bedoelde ratio aantasten!!!

Een buigslappe voorzetwand vertegenwoordigt geen barrière voor de daarop vallende laagfrequente geluidsgolven. Om die reden heeft zo'n constructie ook geen fysieke invloed op de beoogde afmetingsverhouding, die nog altijd door de begrenzende stenen muren van de ruwbouw zelf wordt gedefinieerd!
Alleen echte begrenzende oppervlakken van de ruwbouw definiëren de netto binnenmaten, en dat zijn in laatste instantie de harde, voor alle geluidsgolven (nagenoeg) ondoordringbare buitenmuren van de ruwbouw zelf.
Overwegingen rondom kwesties die "bruto / netto" afmetingen betreffen hebben vergaande implicaties die al in het ontwerpstadium van de ruimte moeten worden meegenomen om een 'mislukking' bij het realiseren van de juiste ratio na eindafwerking te voorkomen.

In de plattegrond links is bijvoorbeeld te zien dat de beoogde netto binnenmaat -- tevens de berekende optimale breedtemaat -- 676 cm moet zijn. In de beide bovenhoeken van de tekening zie je echter afgestemde basstraps en een schuin verlopende midbasabsorber ingetekend. Tussen deze elementen is daardoor een minimale breedte ontstaan van 530 cm.
Maar omdat het hier om buigslappe constructies gaat zal, vanuit het oogpunt van de optimale ratio, de beoogde breedtemaat van 676 cm op die plek blijven gelden. Deze constructies voor bass-management verstoren ter plaatse NIET de optimale en beoogde breedtemaat van de ruimte.

Hieronder som ik een aantal typische situaties op die je zult tegenkomen als je zelf een ruimte gaat ontwerpen en bouwen, en waarmee je op een goede manier moet zien om te gaan:

• Wanneer in een ruwbouw als eindafwerking een akoestisch systeemplafond, of -- God verhoede het -- een gipsplaten plafond van de bouwmarkt, onder het bestaande plafond wordt opgehangen, waarbij dan tevens een leeg plenum (holle ruimte) van 30cm diepte achter die platen wordt aangehouden, dan zal het plafond van de ruimte alleen optisch met ongeveer 31cm worden verlaagd.
  De feitelijke hoogtemaat van de ruwbouw zal NIET veranderen vanuit het oogpunt van de beoogde ratio! Laagfrequente geluidsgolven gaan namelijk zonder problemen door de buigslappe constructie heen en de bruto binnenmaat blijft tegelijk ook de netto binnenmaat, ondanks de optische plafondverlaging!
  
  Als gevolg van deze plafondverlaging gaat er dus geen 31cm verloren van de bruto kamerhoogte, behalve in optische zin. Dat is ook precies de bedoeling van met name een verlaagd akoestisch systeemplafond. Dankzij deze verlaagd opgehangen plafondconstructie zal er heel veel bruikbare laag- en midlaagabsorptie kunnen optreden, waardoor het galmkarakter van de ruimte voor wel 80% onder controle kan worden gebracht.
  Bij het alsjeblieft altijd te vermijden gipsplafond ontstaat ook een zekere laag- en midlaagabsorptie, maar dat is niet op een manier die gewenst of goed te anticiperen is. In elk geval is de absorptie dan veel te selectief en smalbandig. Zoiets zal in principe een akoestisch foutieve plafondkeuze zijn, waarbij achteraf nog een heleboel nagalmcorrectie nodig gaat zijn die net zo makkelijk vermeden had kunnen worden door wat meer uit te geven aan een verantwoord akoestisch systeemplafond.
  
  

• Wanneer in een ruwbouw-ruimte (zelfgebouwde) afgestemde basstraps of paneelabsorbers moeten worden geïntegreerd, dan mag je deze op dezelfde manier benaderen als de buigslappe wanden hierboven. Paneelabsorbers ontlenen hun werking volledig aan dit principe. De afgestemde basstrap heeft een "ademende voorplaat".
  Opnieuw geldt dus dat ook deze akoestisch actieve elementen in de ruwbouw de ratios van de oorspronkelijke ruimte NIET verkleinen! De afstanden tussen de harde wanden, vloer en plafond van de ruwbouw blijven de afmetingen die de ratio bepalen.
  
  De zijwanden, de voorwand en de achterwand in nevenstaande plattegrond van de voorbeeldruimte zijn volledig voorzien van dergelijke elementen, in combinatie met (verderop te bespreken) akoestische diffusers.
  
  Het is niet denkbeeldig dat er aan de achterzijde 80-100cm diepe basstraps worden ingebouwd, en aan de voorzijde (zie links) eveneens 60-80cm diepe modules. Er gaat in dat geval dus niet 180cm of daaromtrent verloren van de totale lengtemaat van de ruimte door toepassing van deze basstraps.
  Geluidsgolven behoren bij deze elementen juist zonder veel problemen de voorzijde te passeren, om dan door de harde begrenzingen van de ruwbouw zelf te worden gereflecteerd. De lengtemaat blijft behouden met basstraps!
  
  

• Wanneer, in een eenmaal voltooide ruimte, akoestische diffusers aan de wanden en/of het plafond worden aangebracht, zoals ook links te zien is, dan gaan deze hoogstens een te verwaarlozen invloed uitoefenen op de bestaande ratios van de ruimte. Een diffuser heeft voor geluidsgolven een dikte die correspondeert met de dikte van zijn achterwand. Dat zal 12mm zijn.
  Diffusers veranderen de ratios van de ruimte ENIGSZINS en alleen voor wat betreft het oppervlak waar zij worden ingezet.
  Bij toepassing van enkele vierkante meter diffusie op de daarvoor bestemde locaties aan zij-, voor- en achterwand zal dat niet tot problemen leiden voor wat betreft aantasting van de optimale beoogde verhoudingen.
  Toepassing van een kamerbrede diffuserconfiguratie op voor- en/of achterwand veroorzaakt WEL een kleine verandering van de ratio -- de dikte van de achterwand van de diffuser. Hiervoor moet worden gecompenseerd: de bruto lengte van de ruwbouw moet met 1x12 of 2x12mm worden vergroot als één, resp. twee uiteinden van de ruimte kamerbreed met diffusers worden afgewerkt.
  Dit kan het geval zijn in een ruimte waarin dipolaire luidspreker worden opgesteld.
  
  

• Vlakke absorptiepanelen, zelfs al zouden ze 15 of 20cm dik zijn, beïnvloeden de ratios NIET. Je weet nu zelf waarom: geluidsgolven dringen hier moeiteloos in door, en dat is precies ook de gedachte achter deze vorm van absorptie.
  
  

• MAAR... alle MASSIEVE materialen die tegen de wanden en het plafond, alsmede op de vloer worden aangebracht, zullen WEL de ratios wijzigen en daarmee moet dus vooraf rekening worden gehouden bij het verschil tussen bruto en netto binnenmaten!
  
  Een lambrizering, bijvoorbeeld, bestaat meestal uit massief plaatmateriaal van een gegeven dikte, en dit wordt direct op de bestaande wand aangebracht. Geluidsgolven zullen hier niet in kunnen doordringen, maar zullen hierdoor worden gereflecteerd. De ruimte wordt er dus iets kleiner door gemaakt...
  Indien lambrizering wordt aangebracht op zijwanden, zul je dus tweemaal de dikte ervan in mindering moeten gaan brengen op de bruto breedtemaat. Ofwel: de bruto breedtemaat van de ruwbouw moet iets breder worden gebouwd, om straks met lambrizering op de juiste netto binnenmaat van de beoogde ratio uit te komen.
  
  Een ruwbouw, waarbij als eindafwerking de wanden zullen worden gestuct zal 2 tot 3cm smaller en/of korter kunnen worden door dit stucwerk en ook 1 tot 2cm lager. Ook dit fenomeen moet dus van tevoren worden ingecalculeerd, omdat het WEL een begrenzende maatregel is, waardoor de ratio zich enigszins zou wijzigen als er niet op voorhand rekening mee werd gehouden.
  
  
  naar boven
  
  

Verder optimaliseren
van een veelbelovende ratio

De eerder al gebruikte rekenmodule om optimale afmetingsverhoudingen te vinden en verder te optimaliseren komt vanaf dit punt weer in beeld. Het nut van deze module gaat verder dan de berekening van een individuele afmetingsverhouding.

Door het opgeven van minimale en maximale begrenzingen bij de berekeningen kun je eveneens inzicht krijgen in globale gebieden waar zowel veel als weinig goede ratios aangetroffen worden, binnen de totaliteit van de opgegeven begrenzingen.

Gebieden met optimale ratios worden aan twee kanten omgeven door gebieden waarin zeer ongunstige ratios bestaan. Dat impliceert inderdaad dat gunstige ratios meestal in groepjes bijeen worden aangetroffen, net zoals ongunstige ratios. In feite zal dit verloop parallel opgaan met de veranderende maatvoeringen binnen het opgegeven grensgebied. Het kan daarom betekenen dat er aan de uiterste grenzen van het door jezelf gedefinieerde grensgebied GEEN gunstige ratios te vinden zijn, maar dat je die dan ofwel in net iets geringere afmetingen moet zoeken, ofwel in net iets grotere. Die laatste zijn dan natuurlijk niet toegestaan, omdat ze groter zijn dan het opgegeven grensgebied, maar iets kleinere maten zullen altijd wel kunnen worden uitgevoerd in de praktijk van het bouwen.

Ook kun je met de rekenmodule berekeningsrondes uitvoeren binnen relatief nauwe begrenzingen.
Zo onderzoek je dan in meer detail één van de gebieden die tijdens berekening met ruimere grenzen werden aangetroffen, maar nog niet rekentechnisch uitgediept werden.
Het resultaat zal opnieuw een aantal ratios kunnen zijn die eruit springen en dus veelbelovend zijn.
Veelbelovende ratios moeten worden genoteerd, om ze later verder te kunnen onderzoeken en te bezien of ze in aanmerking komen om verder te optimaliseren.

De laatste fase van je ratioberekeningen omvat de feitelijke optimalisatie van één individuele ratio, eventueel tot op het niveau van het centimeter voor centimeter doorrekenen.
Dat leidt ertoe dat je een zo hoog mogelijke score kunt realiseren, en misschien zelfs die een of twee laatste probleemfrequenties helemaal kunt elimineren.

Een volledig optimalisatieproces van een veelbelovende ratio zal hieronder worden uitgewerkt aan de hand van de inmiddels overbekende voorbeeldruimte.

De Voorbeeldruimte

Op dit punt in de uiteenzetting vervolgen we het onderzoek naar optimale ratios, door verder te kijken naar de ruimte met de veelbelovende afmetingsverhoudingen die eerder al voorbijkwam in dit artikel.

Het gaat om een, inmiddels, daadwerkelijk bestaande compromisloze dedicated muziekruimte voor stereoweergave. Er was mij voor het ontwerp van de ruimte carte-blanche gegeven door de eigenaar, opdat een en ander zo compromisloos en neutraal mogelijk kon worden. De enige beperking die mij werd opgelegd bestond uit maximale grensmaten voor de bouwkavel: met name de maximale hoogte werd door een gemeentelijke verordening beperkt, maar dat vormde verder geen beperking voor het zoeken en vinden van optimale verhoudingen voor deze ruimte.

De ruimte werd op de kop af 4 jaar na het uitwerken van het papieren ontwerp in gebruik genomen door de eigenaar, die het grootste deel van de akoestische eindafwerking voor zijn rekening heeft genomen.
En dat is geen geringe prestatie...

Van het ontwerp en bouwproces maakte hij doorlopend foto's, die HIER te bekijken zijn als een chronologisch fotoverslag.

Eerst even terug naar het begin van dit artikel...

De afmetingen van de veelbelovende, maar nog te optimaliseren voorbeeldruimte:

930 x 680 x 320 cm
6 samenvallende axiaalmodi: 56, 77, 112, 131, 153 en 168Hz
score = 219 punten volgens de rekenmodule

Deze verhouding is al tamelijk gunstig, maar kent nog wel 6 probleemfrequenties onder 165Hz (+/- 5%).
Dat mogen er wel een paar minder worden als het mogelijk is...

Het belangrijkste doel bij het optimaliseren van deze potentieel bruikbare ratio is om het aantal van 6 axiaalmodi te reduceren. Dat zal in de praktijk neerkomen op een iets andere ratio die in de buurt van deze maten ligt, maar die uiteraard wel binnen de grensgebieden ligt die door de eigenaar zijn opgegeven. Het streven is om afmetingsverhoudingen te vinden die het grondoppervlak van de bouwkavel zoveel mogelijk dekken, en niet om op een veel kleinere ruimte uit te komen.
Het hoogste streven is uiteraard altijd om een ratio te vinden die geen enkele probleemfrequentie onder 165Hz zal hebben.
Dat zal zeker niet altijd lukken, vanwege genoemde fysieke grenzen die moeten worden opgelegd aan de berekeningen.

Tijdens het optimaliseren zul je dus zeker tegen grenzen aanlopen die verdere verbetering van die ratio door vergroting onmogelijk maken. Als verdere vergroting niet mogelijk is terwijl dit rekentechnisch eigenlijk wel zou moeten, is een verdere optimalisatie van die ene ratio niettemin zinloos.
Zoiets zal verderop ook gebeuren, zoals je kunt zien...

De tabel onder de foto rechtsboven bevat de belangrijkste gegevens van de huidige ruimte.
Ze worden vergeleken met nieuwe berekeningsresultaten die de rekenmodule levert.

Rechts zie je ook de tabel getiteld , "Axial Modes".
Deze maakt direct inzichtelijk bij welke frequenties problemen verwacht kunnen worden, en van welke aard ze zijn. Deze 6 potentiële probleemfrequenties onder 165Hz worden met een X aangeduid. De axiaalmodi boven 165Hz worden eveneens met een X aangeduid, maar spelen geen rol meer in het totale plaatje: ze liggen zodanig hoog dat ze 'ten onder' zullen gaan in de overige (enkelvoudige) resonantiemodi.

Eveneens is rechts te zien dat de laagst liggende samenvallende axiaalmodus op 56Hz wordt gevonden.
Optimalisatie maakt het vaak, maar zeker niet altijd, mogelijk dat deze laagste frequentie verder naar boven zal verschuiven. Het is ook mogelijk dat deze simpelweg verdwijnt, omdat deze altijd door de lengtemaat in samenhang met één van de andere twee maten wordt opgeroepen.
Verschuiving naar boven dan wel volledige eliminatie van de laagste probleemfrequentie is een belangrijk doel van verdere optimalisatie van een veelbelovende ratio.


naar boven

Verkenning van de Omgeving

Het overzicht rechts is een screenshot van de rekenmodule.

Deze tabel toont je de "room dimensional preferences".
Hierin kun je zelf grensgebieden definiëren waarbinnen berekeningen mogen plaatsvinden.

Zoals je ziet wordt nu eerst de directe omgeving van de uitgangsratio verkend. De uitgangsratio is in de rechter kolom, "preferred" aangegeven.
De omgeving wordt verkend door de breedte te fixeren, maar de lengte en de hoogte te laten variëren.
Het doel is om te zien wat er zal gebeuren bij variabele hoogte en lengte.

Buiten het bestek van dit artikel om werden ook de nodige varianten met variabele breedte en hoogte, plus variabele breedte en lengte nagelopen, maar de variabele breedte blijkt hier steeds tot een verslechtering te leiden.
De rechtse grafiek is daarom eigenlijk het resultaat van een klein halfuurtje van berekeningen met allerlei grensgebieden. Hij kwam niet meteen al zo uit de lucht vallen...

In het proces van berekenen en herberekenen met telkens iets andere grensmaten zit feitelijk de truc van de rekenmodule: op een gegeven moment heb je een juiste combinatie van grensmaten te pakken, waarmee je op betere verhoudingen kunt uitkomen.

De rechtse kolom, "preferred", slaat altijd op het scenario dat in het resultaat eronder vetgedrukt wordt weergegeven. De voorbeeldruimte eindigt al meteen ver onderaan (scenario 9).
Overigens is een hoogtespeling van 40cm niet direct "in de buurt" te noemen, maar het ontwerpdoel omvatte een zo hoog mogelijke ruimte, zodat het streven zoveel en zo lang mogelijk gericht blijft op een maximale hoogte.
Bij variaties van een breedtemaat, maar zeker bij die van een lengtemaat, stelt 40cm ineens niet meer zoveel voor...

Er is al meteen een verheugende conclusie te trekken uit deze eerste berekeningsronde:

De scenario's 1 t/m 3 bezitten nog slechts 3 van de oorspronkelijke 6 probleemfrequenties!
Dit aantal werd dus zomaar gehalveerd, waardoor één doel van optimalisatie reeds is gerealiseerd: drie probleemfrequenties vormen geen groot probleem voor een afmetingsverhouding, tenminste niet als ze voldoende hoog liggen.

De veelbelovende ratio is zowel langer als (helaas ook wat) lager geworden en is nu:

960 x 680 x 280 cm
3 samenvallende axiaalmodi: 126, 127 en 180Hz
score = 731 punten

Twee op zichzelf staande probleemfrequenties liggen erg dicht bij elkaar (126 & 127Hz).
Die samenhang levert bijna zeker een probleem op, dat in de voltooide ruimte apart zal moeten worden aangepakt. We zoeken nog even verder, om te zien of er meer uit te halen is...

Zou "korter" beter kunnen zijn?

Wanneer we de ruimte zouden verlengen of verkorten zal dit uiteraard invloed hebben op het resonantiepatroon: het gaat hier om de lengtemaat, en daarmee hangen altijd de diepste resonantiemodi van de ruimte samen.

Het is mogelijk dat door een zekere verkorting van de ruimte het aantal probleemfrequenties verder afneemt. Dat ze evengoed ook kunnen toenemen zie je nu in de tabel rechts gebeuren in deze tweede berekeningsronde.

Alleen de lengtemaat is variabel in de rechtse tabel!

In het berekeningsresultaat blijkt de nieuwe "preferred" ratio weer favoriet te zijn, met afstand ditmaal.

Je ziet ook dat met het afnemen van de lengte het aantal samenvallende axiaalmodi juist toeneemt.
Dat is dubbel ongewenst: we willen een zo lang mogelijke ruimte proberen te realiseren, en we willen zeker niet meer dan drie probleemfrequenties overhouden.

In de context van deze ruimte is een verdere verkorting ongewenst, maar het is wel nodig om middels een proefberekening te kunnen zien wat er zou gebeuren bij zo'n verkorting. Als er namelijk minder probleemfrequenties zouden optreden is dat de prijs van een kleine verkorting wel waard.

Is "verlengen" dan beter?

Je zou het wel mogen verwachten: als de afmetingsverhoudingen blijken te verslechteren bij een verkorting, dan zullen ze waarschijnlijk verbeteren bij verlenging.

Helaas is de werkelijkheid complexer: de beide andere afmetingen (B & H) mogen in deze berekening NIET meeveranderen. Er bestaat beslist een optimale lengtemaat waarbij we op 2 of misschien nog maar 1 probleemmodus zullen uitkomen, maar die ligt waarschijnlijk ergens (onrealistisch) bij 14 meter, in elk geval in combinatie bij een gelijkblijvende breedte- en hoogtemaat.

Opnieuw is alleen de lengtemaat variabel in de tabel rechts.

Bij deze derde berekeningsronde wordt uitsluitend de lengte vergroot.
Niet alleen neemt het aantal samenvallende axiaalmodi toe bij verlenging, maar er komt bovendien al direct een retromodus in beeld!
En zoals je weet moeten die boven alles vermeden worden...

We kunnen de lengte, als primair bepalende factor voor het verder optimaliseren, nu rustig loslaten.

derde berekeningsronde: verlenging geeft echte verslechtering!

Breedte en Hoogte samen verkennen...

Het zou in dit stadium goed zijn om te weten wat er zal gebeuren als de ruimte gelijktijdig breder en hoger gemaakt mag worden.

De grensgebieden voor hoogte en breedte zijn nu variabel in de tabel rechts.

Ze zijn variabel gemaakt binnen realistische grenzen, d.w.z. dat deze maximale breedte in principe in praktische zin mogelijk zou zijn. Ditmaal ligt de lengtemaat vast, hoewel er tijdens deze ronde buiten het bestek van dit artikel nog berekeningen met variabele lengte zijn uitgevoerd. Deze brachten evenwel geen betere resultaten voort.

Dit berekeningsresultaat rechts staat twee belangrijke conclusies toe in relatie tot de voorgaande drie berekeningsronden.

Ten eerste: verbreding van de ruimte bij gelijkblijvende lengte levert geen verbeteringen op.
Het zorgt juist al binnen 2dm voor enorme verslechteringen van de ratio!
Op dit moment weten we echter nog niet of een (kleine) versmalling nog gunstig uit zou kunnen vallen!

Ten tweede: Er is opnieuw een iets betere ratio komen bovendrijven dankzij deze vierde berekeningsronde!
De voorkeursratio is van de eerste plaats verdreven door een nieuwe verhouding,
die gelukkig zelfs een grotere hoogte oplevert:

960 x 680 x 300 cm
3 samenvallende axiaalmodi: 127, 178 en 180Hz
score = 806 punten

De twee op zichzelf staande en dicht bij elkaar liggende probleemfrequenties op 126 en 127Hz, die in de vorige voorkeursratio nog bestonden, zijn nu verdwenen. In plaats daarvan liggen er twee andere, maar wel een heel stuk hoger: 178 en 180Hz.
Hoewel die samenhang in theorie ook een probleem kan opleveren in de voltooide ruimte, zal het door de hoge ligging rond 180Hz heel weinig moeite kosten om dit akoestisch te bedwingen. Naar verwachting zal het daar aanwezige bass-management automatisch al doeltreffend hiermee afrekenen.


naar boven

Verfijnen met centimeters

Tot nu toe hebben we met de rekenmodule steeds gerekend in hele decimeters. De grootste tekortkoming van deze module is dat het weliswaar prima mogelijk is om in centimeters te rekenen, maar dat de module zelf altijd afrondingen op hele decimeters laat zien in de berekeningsresultaten.

Dit hoeft alleen een ernstige tekortkoming te zijn als je het tot nu toe behaalde resultaat van 960 x 680 x 300 cm zou laten voor wat het is. Het is dan weliswaar al een uitstekende ratio om letterlijk op verder te bouwen, maar er valt ook -- zo blijkt aanstonds -- een nog beter resultaat te behalen door met een nauwkeurigheid van centimeters door te rekenen op deze toch al uitstekende basis.
Het blijkt namelijk mogelijk te zijn om uiteindelijk nog maar 2 samenvallende axiaalmodi in plaats van de bovenstaande 3 te realiseren.

De methode om dit te doen is om van één dimensie tegelijk steeds één centimeter te vergroten of te verkleinen, en om dan de individuele ratio te berekenen. Als deze beter is doe je er nog een centimeter bij of af, net zolang tot de ratio niet meer verbetert maar slechter wordt. Je probeert dus eigenlijk of vermindering of vermeerdering van het aantal centimeters verbetering oplevert in één dimensie.

Als verbetering niet meer mogelijk is ga je over naar de tweede dimensie van de drie en probeert weer per centimeter meer of minder of er verbetering te behalen is. Tenslotte doe je het ook met de derde dimensie.

Vervolgens begin je weer helemaal opnieuw met de eerste, dan de tweede en dan de derde, net zolang tot er geen enkele verbetering meer te behalen is door bij om het even welke dimensie nog een centimeter toe te voegen of af te halen. De maximale score is dan blijkbaar bereikt.

Welnu, als je dit dus zou doen met de hierboven gevonden favoriete ratio van 960 x 680 x 300 cm, die beschikt over drie probleemfrequenties en een score van 806 punten, dan zou je uiteindelijk uitkomen op de duidelijk betere ratio die hier rechts is ingevuld in de "preferred" kolom.

De beste ratio die tot nu toe gevonden kon worden is daarmee dus:

971 x 684 x 307 cm
2 samenvallende axiaalmodi: 126 en 178Hz (zie de tabel verderop)
score = 947 punten !!!

Wat je nu dus ook zult zien in het berekeningsresultaat rechts is, dat de ratio die op no.1 is vermeld -- wat tevens de door mijzelf ingevoerde "preferred" ratio is -- door de module gewoon blijkt te worden afgerond op hele decimeters ondanks dat de preferred kolom duidelijk laat zien dat er wel degelijk op de centimeter nauwkeurig werd ingevoerd!

In de "smallest" en "largest" kolommen, eveneens door de gebruiker in te vullen kolommen, zijn de waarden wel door mijzelf op hele decimeters ingevoerd, maar dat is ook de bedoeling.
Maar alle berekeningsresultaten zelf (de "scenarios") kunnen zowel hele decimeters vertegenwoordigen als, -- en dat is vele malen waarschijnlijker -- waarden die eigenlijk op de centimeter nauwkeurig zouden moeten zijn, maar helaas niet op die manier door de module worden getoond...

Het zal daarnaast wel duidelijk zijn dat verfijnen met centimeters, zoals ik dat heb genoemd, zeer de moeite waard kan zijn! Het elimineren van één van de drie resterende axiaalmodi en het winnen van maar liefst 140 scorepunten extra is bepaald niet niks.
Dit is ook meteen de reden dat je zomaar een uurtje of 5 bezig kunt zijn om alle opties die werkelijk op je bouwkavel zouden passen goed na te lopen en zorgvuldig door te rekenen.
Aangezien je dit slechts één keer zult hoeven te doen, lijkt me dat geen al te zware opgave. Het is wellicht een grotere opgave om eerst goed te leren omgaan met de module zelf, maar als dat eenmaal wil lukken is ie zijn gewicht en alle moeite in goud waard...




Grensgebieden

In de tabel rechts werd tegelijk ook een maximaal uitgebreide berekening gedaan met variabele grensgebieden in alle drie de dimensies tegelijkertijd.
Dit om te kunnen zien of er mogelijk een nog betere ratio wil komen bovendrijven.

Zoals eerder gingen ook hier, buiten de context van dit artikel om, de nodige extra berekeningen aan vooraf, waarbij steeds minimaal verschillende grensgebieden werden gedefinieerd, voordat de rechtse tabel op deze manier kon worden gegenereerd. De sleutel voor een bruikbaar berekeningsresultaat is dus ook gelegen in het invoeren van de juiste grensgebieden.

Het berekeningsresultaat rechts maakt nu betrouwbare eindconclusies mogelijk...

• Bij verlenging ontstaat er direct een retromodus.
  Dat is altijd erg kwalijk en die laten we, zoals eerder al duidelijk werd gemaakt, met rust.
  Ratios met retromodus vallen in principe altijd af.
  
  
• Versmalling blijkt ook geen soelaas te bieden.
  Iets wat we ons daarnet nog hardop hebben afgevraagd, maar wat we nu kunnen loslaten.
  
  
• Bij verlenging loopt het aantal samenvallende axiaalmodi nog verder terug!
  Bij 10,9m is er nog maar 1 over, maar dat is dan wel in combinatie met slechts 2,6m kamerhoogte.
  Daardoor valt die optie simpelweg af; het is te laag voor een ruimte zoals deze, waarin een groot luidsprekersysteem moet worden geplaatst. Daarnaast is er op 10,9m ook een retromodus in beeld, die mogelijk wel zou kunnen verdwijnen door verfijning op het niveau van centimeters, maar de ontoereikende kamerhoogte blijft altijd bestaan.
  Kortom: een verdere verlenging is hier niet zinvol.
  
  
• De belangrijkste conclusie uit de vijfde en laatste berekeningsronde is daarom:
  De huidige favoriete ratio lijkt het maximaal haalbare te zijn binnen het onderzochte gebied, maar ook ruim daar omheen. Het lijkt ook de meest geschikte optie te zijn die voldoet aan de door de eigenaar gestelde eisen rondom maximale lengte, breedte en hoogte van zijn ruimte en bouwmogelijkheden.
  Om betere ratios te vinden zullen de toegestane grensgebieden moeten worden overschreden, en dat is geen optie omdat onwrikbare ambtenaren dan zullen wijzen op hun ambtelijke grenzen.
  
  
  
  
  
  
  

De favoriet analyseren

De in alle opzichten geoptimaliseerde ratio blijft:

971 x 684 x 307 cm
2 samenvallende axiaalmodi: 126 en 178Hz (zie de tabel verderop)
score = 947 punten !!!

De grafiek rechts, die de verdeling van resonantiemodi over de lage frequentieband toont, laat zien dat het aantal modi vanaf de tertsband met 31,5Hz als centrale frequentie groter is dan NUL is. In de twee lagere tertsbanden komen dus geen samenvallende axiaalmodi voor die een potentieel probleem kunnen worden.
Vanaf t.b. 31,5Hz loopt het aantal modi per 1/3 oktaaf fraai en geleidelijk op, precies zoals dat ook de bedoeling is bij een optimale ratio.

Er valt op deze grafiek verder niets aan te merken. Je mag het een modelgrafiek noemen...

In de grafiek is niet de aanwezigheid of locatie van de 2 overgebleven, potentieel lastige axiaalmodi terug te vinden. Wel is zichtbaar dat er nergens een retromodus aanwezig is.

De tabel rechts, screenshot van de rekenmodule, laat de algemene gegevens zien van de favoriete ratio.

Slechts twee samenvallende axiaalmodi onder 165Hz zijn uiteindelijk overgebleven.
Bij de aanvang van de optimalisatie waren dat er nog zes.

Dat is al met al een heel goed resultaat, al zou een aantal van NUL nog beter zijn. Vaak is dat ook mogelijk, maar vanwege de opgelegde grenzen is dit het hoogst haalbare.

We willen nu ook nog graag weten op welke frequenties de 2 modi liggen en of daar eventueel nog problemen mee kunnen worden verwacht.

De tabel met "Axial Modes" rechts toont verheugend nieuws.

De laagste potentiële probleemmodus voor deze grote ruimte blijkt op 127Hz te liggen -- relatief erg hoog en dat is gunstig omdat een eventueel probleem in dit frequentiegebied met fysiek ondiepe maatregelen kan worden ingepast in het toch al toe te passen bass-management.

Op 178Hz bevindt zich de tweede resonantiemodus. Hiervoor geldt in principe hetzelfde als voor bovenstaande modus op 127Hz.

Het is duidelijk dat eventuele ratio-gerelateerde problemen gemakkelijk te elimineren zijn.
Dat komt omdat ze erg hoog liggen, omdat ze mild van aard zijn en omdat het gangbare bass-management dat in deze ruimte zal worden ingebouwd krachtig genoeg zal zijn om er vanzelf mee af te rekenen. Separate actie voor problemen op 127 of 178Hz zijn niet te verwachten.

Je herinnert je vast nog dat de laagste modus van de oorspronkelijke veelbelovende ratio op 56Hz lag. Maar ook op 77, 112, 131, 153 en 168Hz waren er samenvallende modi.

Al met al is er dan toch sprake geweest van een heel zinvolle optimalisatie van een potentieel al behoorlijk gunstige ratio...

En Nu???

Is de kous van het optimaliseren hiermee nu af, zul je je misschien afvragen...

Als we teruggaan naar de eerste berekeningsronde van de optimalisatie -- rechts -- zie je dat de bovenste ratio 9,6 x 6,8 x 2,8 degene is die we zijn gaan optimaliseren, en die uiteindelijk resulteerde in de favoriete ratio hierboven.

Eronder, op plaats 2 en 3, zie je twee andere ratios die eveneens uitstekend zijn omdat ze bij aanvang over slechts 3 potentiële probleemfrequenties beschikken. We hebben daar in dit voorbeeld verder niets mee gedaan en ikzelf heb er evenmin ooit iets mee gedaan.

Ze zijn al wel meteen gebaseerd op kamerhoogte 3,1m en op een iets geringere lengte.
Zoiets zou ook op het bouwkavel in kwestie passen, is nog steeds best "groot" te noemen, maar gaat net wat minder centjes kosten want een stukje kleiner.
Misschien is het zelfs mogelijk om één van deze twee ratios (of beide) zover te optimaliseren dat er slechts één of nul probleemfrequenties overblijven. Je zult het pas weten als je het gaat uitrekenen, want het is niet op voorhand te voorspellen...

Praktische, concrete en budgettaire afwegingen zijn legitiem en je weet nu ook dat je met de rekenmodule net zo makkelijk ook een van de iets kleinere ratios kunt optimaliseren. Het eindresultaat zal altijd zeer goed zijn. Meestal, zo ook in dit geval, zal de eigenaar willen streven naar een zo groot mogelijke ruimte op de beschikbare kavel.
In principe zal een grote ruimte ook betere opties bieden voor optimale weergave dan een kleinere, mits ze beide over gunstige of optimale ratios kunnen beschikken.

Conclusie

In de context van het ratio-onderzoek voor deze muziekruimte heb ik uiteraard nog gekeken naar verdere mogelijkheden voor vergelijkbare afmetingsverhoudingen. De maximale hoogtegrens was bijvoorbeeld 350cm inwendig, en de maximale lengtemaat was precies 10 meter.
Meer dan wat "rommelen in de marge" bleek hier niet mogelijk te zijn, terwijl ik mijn zinnen persoonlijk wel had gezet op een grotere hoogte dan die uiteindelijk werd geïmplementeerd. Dat had vooral ook te maken met de forse, diepe plafonddiffusers die zouden worden aangebracht, en die het plafond zeker in optische zin zouden verlagen. Niettemin is het uiteindelijk resultaat, na er zelf ook met eigen oren te hebben kunnen luisteren, boven verwachting en in muzikale zin onwaarschijnlijk bevredigend gebleken. We zullen nooit weten hoe goed een hogere ruimte zou zijn uitgevallen, maar soit... wat niet weet, wat niet deert...

Hiermee komt een einde aan een artikel dat een uiterste poging is geweest om het meest vage onderdeel van akoestiek inzichtelijk te maken, en wel dat van de afmetingsverhoudingen.
Ik hoop dat het zodanig inzichtelijk kon worden gemaakt dat je er IN DE PRAKTIJK zelf iets mee kunt doen, mocht dit binnen je plannen en mogelijkheden liggen.

Meermalen duidde ik er al op dat de downloadpagina de rekenmodule levert waarmee alle berekeningen in dit artikel (en in de 13 jaren ervoor) door mij werden gedaan. Je zult hier in het begin behoorlijk mee moeten oefenen, om dan op een gegeven moment aan te gaan voelen hoe de module het beste voor je werkt. Hij kan in elk geval in engelse maten (feet) alsook in onze gangbare maten (meters) werken, maar dat moet je dan wel even zien en tevoren instellen!

Verwacht niet dat er altijd en als vanzelf een absolute topratio boven komt drijven bij elke berekening die je doet! Ik gaf dat in het artikel ook expliciet aan: de getoonde tabellen waren dan het resultaat van een serie berekeningen buiten de context van het artikel om, die uiteindelijk leidden naar die ene tabel die werd ingesloten.
Je doet in de praktijk een hele serie berekeningen, en je maakt notities van veelbelovende opties, omdat jij of het programma ze anders zal vergeten. Zo'n serie toont je op een gegeven moment een patroon, zodat je weet in welk gebied of in welke van de drie dimensies je de betere verhoudingen zult kunnen vinden. Veelbelovende ratios die uit de berekeningen springen zul je dus steeds moeten opschrijven, anders zullen ze bij een volgende berekening net zo makkelijk onvindbaar blijken...

Topratios worden niet per definitie steeds weer getoond of altijd automatisch gevonden bij ELKE berekening. Zelfs niet al liggen ze binnen de opgegeven grensgebieden!

Deze rekenmodule heeft zo z'n mysterieuze kanten, en daar moet je het mee zien te doen.

Elke potentieel zinvolle ratio zul je vervolgens verder moeten optimaliseren (verfijning per centimeter!), om te zien hoe goed ie werkelijk kan worden. Dat kan de module niet voor je doen.
In het begin optimaliseer je met decimeters tegelijk, maar op een gegeven moment ontstaat ook de behoefte om in centimeters te werken om ook de laatste probleemfrequentie (hopelijk) weg te kunnen werken.
Dat zal sneller en vanzelfsprekender werken naarmate je de module beter leert kennen en aanvoelen.

Als schrijver van het artikel en als degene die deze rekenmethode voorstelt sta ik open voor het geven van relevante nadere informatie over deze materie.
Mocht je bepaalde problemen tegenkomen of dingen niet helemaal zeker weten, aarzel dan niet om een mailtje te sturen naar readscapes@xs4all.nl

Ik zal helpen waar mogelijk!



Toine Dingemans, 26 januari 2018.



naar boven